This paper is accepted to NIPS 2009. (Currently mainly called NeurIPS.)
2. Discovery of Hidden Causes for a Benchmark Dataset
Authors desinged a simple network that is working on MNIST dataset.
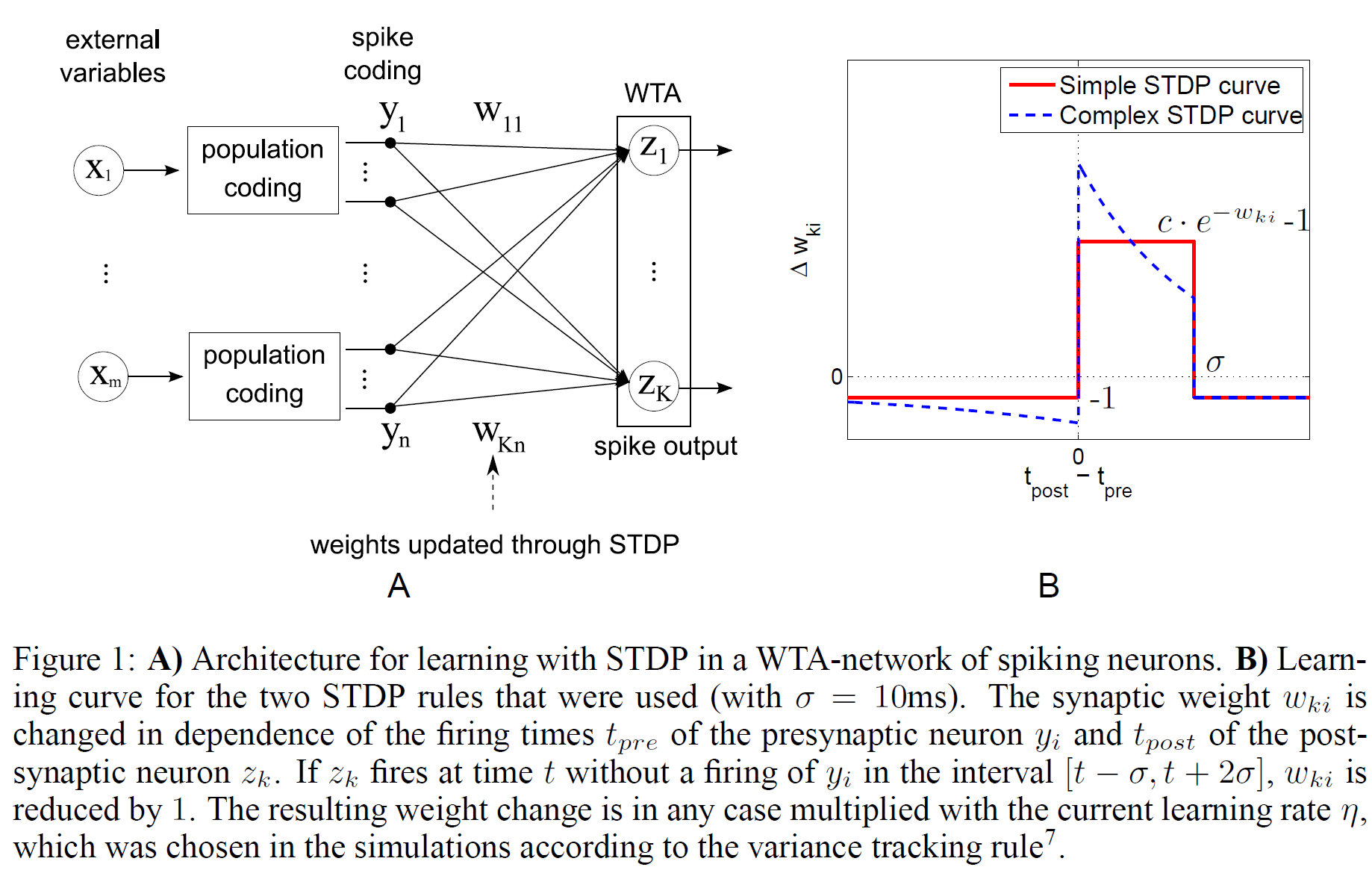
Population coding is utilized to encode real-valued input variables $\underline{\underline{x}}$ into binary-valued input $\underline{\underline{y}}$. More detailed explaination will be in section 3. Moreover, winner-takes-all (WTA) mechanism is applied to this architecture. There is one thing notable in WTA is the winning probability of each neuron, which follows softmax distribution:
\[p(z_{k,t}=1|{\bf y}_t) = \frac{ \exp(w_{ki}\tilde{y}_{ti}+w_{k0}) }{ \sum_{k'=1}^K\exp(w_{k'i}\tilde{y}_{ti}+w_{k'0}) }\\ \ \\ \text{such that}\\ \ \\ \tilde{y}_{ti} = \begin{cases} 1\qquad\text{if }\exists_{\ t-10\le t'\le t}:y_{t'i}=1\\ 0\qquad \text{otherwise.} \end{cases}\]Einstein summation convention is used to represent matrix multiplication.
But, why does $\tilde{y}_{ti}$ reflects the spikes of past? Authors say that it is a representation of EPSP, to facilitate the theoretical analysis henceforward. It does not affect the training of the SNN.
3. Underlying Theoretical Principles
Prior to looking at the analysis, allow me to formulate definitions and properties used within this paper. Some variables are changed for more legibility.
\[\begin{align*} w_{ik}:&\text{weights from presynaptic $i^{\text{th}}$ neuron to postsynaptic $k^{\text{th}}$ neuron.}\\ b_k:&\text{threshold of postsynaptic $k^{\text{th}}$ neuron.}\\ \mathcal{N}_{\underline{\underline{w}}}:&\text{stochastic artificial neural network.}\\ \underline{x}\in\{0,1\}^{M}:&\text{pixel values. Each is binarized from MNIST pixel brightness.}\\ \underline{\underline{y}}\in\{0,1\}^{T\times mM}:&\text{population-coded input with Poisson distribution.}\\ \underline{\underline{z}}\in\{0,1\}^{T\times K}:&\text{output vector such that }\forall t:\underline{z}_t\in\left\{z'\middle|\sum_{k=1}^K z_{tk}=1\right\}\\ p\left(\underline{z}_{tk}=1\middle|\underline{y}_t,\underline{\underline{w}}\right)=&\frac{ \exp\left( w_{ki}y_{ti}+b_{k} \right) }{\sum_{k'=1}^K{ \exp\left( w_{k'i}y_{ti}+b_{k'} \right) }} =\left( \text{softmax}\left( \underline{\underline{w}}\,\underline{y}_t+\underline{b} \right) \right)_k \end{align*}\]But, how does $\underline{\underline{y}}$ encoded? First, the pixel brightness of MNIST image is binarized to $0, 1$, making the binary input $\underline{x}$. This process removes some unimportant pixels (only $\le5%$ of the data is black in them). Second, encode $x_i$ into one-hot vector $y_{t,0},y_{t,1},\cdots,y_{t,m-1}$. For instance, for black pixel i, $x_i=0$, $\underline{y}_{t, [M(i-1),M(i-1)+1]}=(1,0)$. In this case, m=2, the same as in this paper. In fact, there are more population coding methods, but not used in this paper. (Wikipedia-Neural Coding)
WIP.